Диаграммы Эйлера-Венна

Диаграмма Венна — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств. Если пересечения позволяется указывать не все, получается более общий случай — круги Эйлера.

Диаграммы Эйлера — Венна (как их ещё называют) изображают все комбинаций свойств, то есть конечную булеву алгебру. При 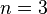диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной вЛондоне в 1881 году.

Для наглядности логические высказывания изображают диаграммами Эйлера-Венна. Любое высказывание на диаграмме изображают кругом, а его отрицание - частью плоскости, находящейся вне круга.
Для составного высказывания, состоящего из двух элементарных А, В, на диаграмме изображают два перекрещенных круга и штрихуют зоны, соответствующие элементарным высказываниям. Цветом выделяют зону, соответствующую составному высказыванию. Для составных высказываний, связывающих элементарные с помощью логического "ИЛИ", в цветную зону попадает вся заштрихованная область. Для составных высказываний, связывающих элементарные с помощью логического "И", в цветную зону попадает область двойной штриховки (решетка). К логическому "ИЛИ" часто применяют пермин "ЛОГИЧЕСКОЕ СЛОЖЕНИЕ", а для графического понимания - "ОБЪЕДИНЕНИЕ". К логическому "И" применим термин "ЛОГИЧЕСКОЕ УМНОЖЕНИЕ", а для графического понимания - "ПЕРЕСЕЧЕНИЕ". 

Составим диаграммы Эйлера-Венна для высказываний.

СОСТАВНЫЕ ВЫСКАЗЫВАНИЯ СОСТАВЛЕННЫЕ ИЗ ЭЛЕМЕНТАРНЫХ А, В

СОСТАВНЫЕ ВЫСКАЗЫВАНИЯ СОСТАВЛЕННЫЕ ИЗ ЭЛЕМЕНТАРНЫХ НЕА, В

Задачи для самостоятельного решения

Задача № 1

 Составить диаграммы Эйлера-Венна для составных высказываний:





Среди диаграмм есть одинаковые. Выпишите составные высказывания с одинаковыми диаграммами.

Задача №2

В классе 45 учащихся. Из них 15 человек не увлекаются спортом, а те, кто им занимается, распределены следующим образом: 21 — лыжни­ки, 19 — велосипедисты, 12 — пловцы. Известно, что 18 учащихся увлека­ются лыжами и велоспортом, трое — плаванием и лыжами, а один — велоспортом и плаванием. Сколько учащихся занимается только плаванием? Лыжным спортом? Велоспортом?

Задача № 3

В классе 14 лыжников, 6 пловцов и 13 велосипедистов. Пятеро занимаются лыжами и плаванием, трое — велоспортом и плаванием, трое — лыжами и велоспортом, а двое занимаются сразу тремя видами. Сколько учащихся занимается только плаванием? Только лыжами? Только велоспортом  Сколько учащихся в классе, если известно, что десять учащихся спортом не увлекаются'?

Задача № 4

 В классе 35 учеников. Среди них: 16 велосипедистов, 17 лыжников, 10 пловцов. Пятеро увлекаются лыжами и велоспортом, трое — плаванием и лыжами, трое — велоспортом и плаванием, а двое занимаются всеми ви­дами спорта. Сколько человек в классе не увлекаются ни одним из названых видов спорта?